xy平面上の曲線Cは媒介変数θを用いて
\[x=\dfrac {1}{3}\cos \theta +\dfrac {2}{3}\sin \theta\]
\[y=\dfrac {1}{6}\cos \theta -\dfrac {2}{3}\sin \theta\]
と表される。このとき
(1)Cを表すｘとｙの関係式を求めよ。
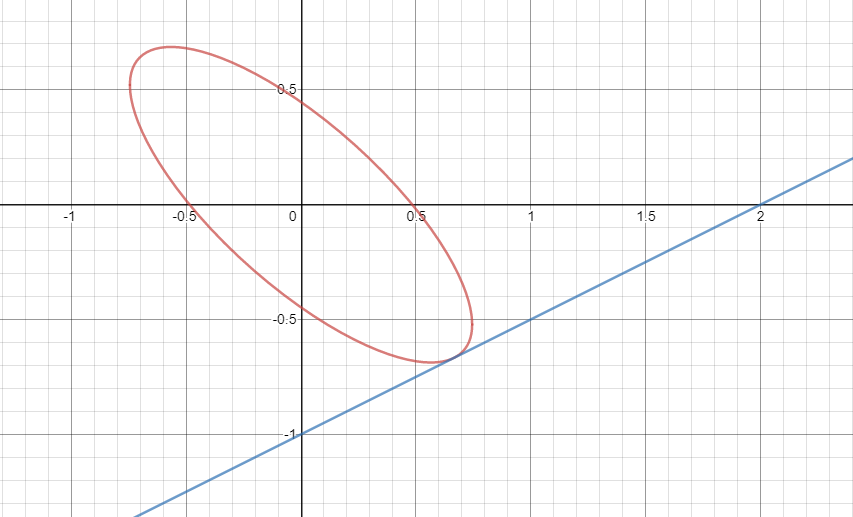
(2)点（2,0）から曲線Cに引いた接線の方程式と接点の座標を求めよ。（0≦θ≦π）
θが媒介変数になっているので、ｘとｙの関係式が導けますね。
楕円になりそうです。
接点がわかっているときの
楕円の接線の公式なら習ったよ
今回の問題は接点がわからないし楕円が回転しているケース
どうやったらいいかな？
直線の式をy=ax+bと置いて連立方程式を作るとか
なるほど。接するから2次方程式の
重解条件で攻めるんだね
あれ？計算がとんでもなく面倒くさい！！！
連立方程式でも解けそうだけど、やってみたらとんでもなく面倒くさい！
ちょっとした工夫ですんなり解けます。
（1）はcosθとsinθの連立方程式のように考え式変形を行います。
これを次の関係式に代入します。
すると、次の関係式が導かれます。（楕円が回転した形ですね）
と、まあここまでは単なる式変形なので軽く出せる人も多いでしょう。
では続いて(2) について
何も思いつかないときは、接線の式をy=ax+bと置いて(1)の曲線との交点が一つであることから判別式D=0としても解けます。でも、実際に計算すると思ったよりも面倒で時間がかかり、これが入試本番だったら心が折れてしまうかもしれません。
私も実際どれぐらい時間がかかるのか試してみましたが…私の計算力で10分程度でした。
ではここからが本題。X＝cosθ、Y＝sinθとして、新しいXY平面を考えます。
の式に代入すると
単位円を表すのがポイント
と、原点中心で半径が１の円になります。
(x,y)=(2,0)は、X=4 Y=1に移ります。
（X,Y)=(4,1)から、原点中心で半径が１の円に接線を引くと、接線はY=１、接点は（0,1）とうことがすぐにわかるので、これをx,yに戻すと接線は
となることがわかります。接点は次の通りです。
（もう一本接線が出来るのですが、θの範囲からY＝１だけに限定されるのが出題者の心配りですね）
あ、優しい…
数学は解けるように出来ている
（寺田文行先生の口癖だよ）
寺田文行先生って誰？
「数学の鉄則」シリーズで有名な早稲田大学の
寺田文行先生を知らないの？
あの鉄則シリーズの先生かあ。
プリクマ先生がよく
「数学は解けるように出来ている」って
言うのは、寺田先生の受け売りなんだね。